Value-at-risk

Value-at-risk, also know as VaR, is a metric introduced by JP Morgan indicating the total risk of a portfolio in a single number. In technical terms, value-at-risk indicates that with a certain probability, over a given period of time, the loss of a portfolio will not be greater than x. For example, the VaR for 10 days with 99% could be 1,000,000. Meaning that, with 99% certainty, the loss of the portfolio of 10 trading days, will not exceed 1,000,000. Important is that the VaR does not indicate how much the loss will be when the unfortunate 1% is happening.

Technical value-at-risk description

In mathematical terms, the equation below describes the definition of value-at-risk: the loss which will not be exceeded with a certain probability during some period of time.

$P(x < X) = \int_{- \infty}^{X} f(x) dx = p$

Based on the normal distribution, this can through normalization be more simply written in the following way.

$P(x < X) = P(Z < \frac{X - \mu}{\sigma}) = p$

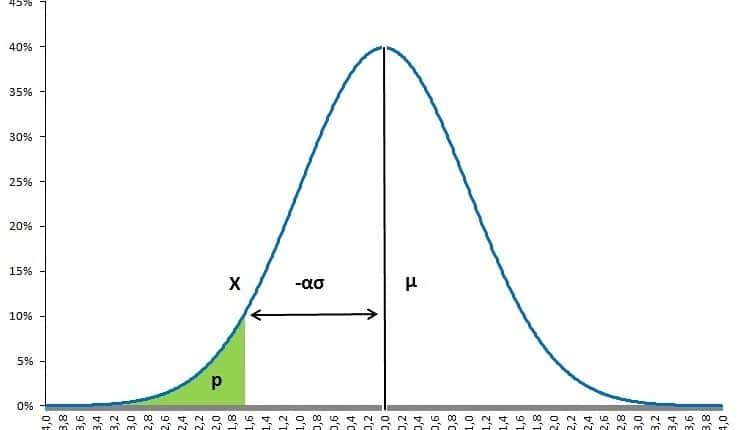
Intuitively, both formulas just measure the area under a density curve, for example a normal distribution as shown in the figure below.

Parametric value-at-risk

One of the most commonly known VaR models is the parametric value-at-risk model. This type of VaR is often used to measure risk in linear derivatives, forwards, futures and swaps. This model is based on the normal distribution, and just needs an estimate of volatility and the mean if required. In order to calculate a VaR, you first need to estimate the portfolio’s or security’s volatility, σ, the money invested in the portfolio or security, W, and if required the expected return, μ. Additionally, it is required to set a certain probability and time horizon. Based on the normal distribution, the values of α will equal 1.282, 1.645 or 2.326 when fixing the probability on 90%, 95% and 99% respectively.

$VaR_{p,t} = \mu \cdot W - \alpha_{p} \cdot \sigma \cdot W$

Obviously, the main benefit of this model is its simplicity. Without any additional estimation, a VaR on a different time horizon and,or a different probability can directly be derived from the same information. The downside is that the assumed normal distribution may not be true which can be accommodated by assuming a t-distribution allowing for fatter tails.

Historical value-at-risk

Another simple way to calculate value-at-risk without making any distributional assumptions is by using historical values. Historical value-at-risk provides an additional benefit of having a better tail risk measure for nonlinear contract such as options.Just as the names suggest, historical returns, both positive and negative, are used to estimate future possible returns. A value-at-risk can for example be gathered by gathering historical portfolio returns and sorting them from small to large. The x% smallest value multiplied by your investment equals the historical VaR.

Monte Carlo value-at-risk

Monte Carlo value-at-risk can also be estimated through simulation. This method is more complex and requires to draw randomly from an assumed distribution, normal, t-distribution or others. This method also allows tail risk estimation of nonlinear contracts, option. It provides an additional benefit of being able to construct a sufficient amount of observations in the tail. The downside is that simulated value-at-risk is more time consuming. Moreover, The VaR estimate is only correct if the chosen distribution from which numbers are drawn from is the right one.

Summary

value-at-risk a tail risk measure indicating a non-loss exceedance over a certain period with a certain probability. VaR can be calculated in various ways: parametrically, historically and based on simulations.