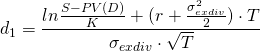Black Scholes option pricing model
The Black and Scholes option pricing model provides an analytical solution to value european call and put options. Initially, the valuation model could only be used for non-dividend paying shares, later on the model was modified to incorporate dividend payments. Additionally this model improved risk management capabilities through the construction of the greeks.
Basic Black Scholes option pricing model
In order to value european option, 5 key ingredients are required. First the model needs the spot price, S, and the strike price K of the contract. Next to this, the risk free rate r, in continuous compounding, needs to be plugged in together with the time T of the contract and the volatility σ of the underlying.
With
In case of european puts, the valuation formula based on put-call parity becomes as follows:
Black Scholes option pricing model and dividends
When dividends are paid during the lifetime of the european option, the price of the call option has to be adjusted. This extends the previous model to:
In case of approaching te dividends as a continuous yield, q, to basic model becomes:
Summary
European call and put option can be valued through the Black Scholes option pricing model. Spot and strike price, risk free rate, time and volatility are the key ingredients for a valuation exercise.
Black Scholes option pricing model Excel implementation
Need to have more insights? Download our free excel file: Black Scholes option pricing model.