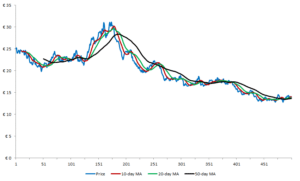
Moving average
Moving averages are among the most popular quantitative trading rules. This is possibly explained by their simplicity and ease of use. In practice, there exist a number of them. These can be classified into simple, weighted and exponentially weighted. In any case, these various trading rules are very similar but differ in their weighting scheme of past prices.
Moving average calculation
A moving average indicator can be calculated in the following straightforward way. First assuming the weighting scheme is equal over every data point, the indicator boils down the the simple moving average. Thereafter, a lag parameter needs to be imposed which determines the amount of past prices is used to calculated the moving average. These are for example, 20 ,50 or 200 past prices although any value can be used to calculate.
Dual moving average
A dual moving average trading system uses 2 indicators to generate buy and sell signals. The first moving average uses a smaller lag parameter. As a result, this indicator will more closely follow the current asset price, although it will also evolve more erratic over time. The second indicator uses a larger lag parameter and thus evolves more smoothly over time but follows less recent price changes. Technical analysts argue that the crossovers generates buy signals whenever the short moving average crosses the long one from below upwards. Sell signals are generated when the short moving average crosses the longer one from above downwards.
Moving average formula
How to calculate moving averages? Simply it can just be calculated as follows. First determine the lag parameter, x, then sum the past x price series you can observe today and divide this sum by x. Do this for every day in you sample where is the past observations is at least x. The obtained price series is the evolution over time.
Summary
One of the most simple and most popular technical trading indicators are moving averages. Technical analyst use these to identify trends in price series and guide their buy and selling activity. These indicators require a certain lag parameter. A combination such a trading rule with a short and long lag parameter is called a dual moving average trading system.
Moving average
Want to have an implementation in Excel? Download the Excel file: moving average