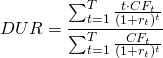Duration
Duration is an important concept for fixed income securities. It is a time-weighted average of the future cash flows. Duration is used as a measure of interest rate risk. The higher the duration of a bond, the higher its sensitivity to interest rate changes. This means that the higher a bond’s duration, the larger the impact of a change in the interest rate on the value of the bond.
Calculation
Duration (DUR) can be calculated as the sum of time-weighted discounted cash flows (CFt), divided by the sum of discounted cash flows. The formula is below
The term in the denominator is nothing more than the value of the bond. We can thus rewrite the above formula to obtain
Effect of maturity
The relationship between duration and a bond’s maturity is simple. The longer the time until maturity, the higher the duration of a bond be. The value of a bond with a long time till maturity will therefore be more sensitive to price changes than a similar bond with a lower time till maturity.
Effect of coupon rate
A bond’s coupon rate and duration also have a clear relationship. The higher the coupon rate of a bond, the lower its duration. This is because higher intermediate cash flows are received before maturity. This makes the bond less sensitive to interest changes, because the investor receives part of the present value of the bond early. As a special case, the duration of a zero-coupon bond is the same as its maturity. This is because of the absence of any interim cash flows during its lifetime.
Summary
Duration measures a bond’s sensitivity to interest rate changes. The higher the duration, the more interest rate sensitive the bond. Bonds with longer maturities and lower coupon payments have higher durations.
Duration Excel implementation
Need to have more insights? Download our free excel file: duration.