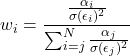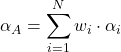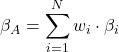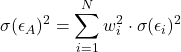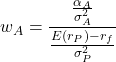Treynor-Black Model
The Treynor-Black model is an asset pricing model proposed by Fischer Black and Jack Treynor in an article titled “How to Use Security Analysis to Improve Portfolio Selection” that was published in the Journal of Business in 1973. The model can be used to engage in active portfolio management.
The optimal risky portfolio under the Treynor-Black model consists of a passive (market) portfolio and an active portfolio for which we have alpha forecasts. These alpha forecasts can be obtained using for example a factor model. At the bottom of this page, we provide an Excel example that implements the Treynor-Black model.
But before we turn to the Excel file, let’s first go over the relevant steps.
Step 1
Under the Treynor-Black model the first step is to determine the weights of the securities in the active portfolio. The weights we assign to the securities should be proportional to:
![]()
where σ(εi)2 is the volatility in the security’s price that is not due to changes in the factors, i.e. unsystematic risk. Hence, the weight assigned to a particular security will be such that:
- the higher the alpha of the security, the higher the weight we assign to the security,
- the more volatile the security is, due to firm-specific news, the lower the weight.
The ratio of alpha to nonsystematic risk is called the Treynor-Black ratio or appraisal ratio. The appraisal ratio measures the value the security would add to our portfolio, on a risk-adjusted basis.
The optimal weights under the Treynor-Black model are:
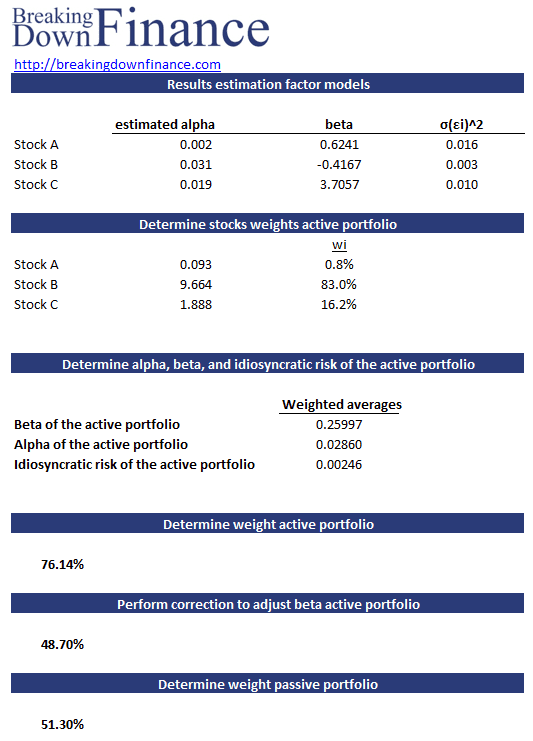
Using these weights we can construct the active portfolio and calculate the corresponding αA, βA, and the σA2:
Step 2
Next, we need to determine the size of the optimal portfolio (wA) in the overall portfolio. Treynor and Black show that the weight of the active portfolio should be:
where rP is the return on the passive portfolio, rf is the risk-free rate and σP2 is the volatility of the passive portfolio.
Up to now, we have not yet used the βA of the active portfolio. It is possible that the active portfolio we have obtained exhibits a lot of systematic risk, i.e. a high beta. To avoid our overall portfolio from becoming too risky, we make a small correction. That way, we ensure that the portfolio beta of the overall portfolio doesn’t change. The correction looks as follows:
As such, the overall portfolio consists of an active portfolio with weight wA and a passive portfolio with weight wP = 1-wA.
Treynor-Black model advantages
If we can successfully identify securities with positive alphas, the combined portfolio will lie above the efficient frontier using Markowitz’s portfolio selection approach.
This will allow us to obtain a steeper capital allocation line and thus better risk-adjusted returns. The extent to which we can improve returns depends crucially on our stock-picking abilities, i.e. our skill at identifying ‘alpha’.
Treynor-Black Example
The table below illustrates the approach using Excel. The link to the example can be found below.
Summary
The Treynor-Black model is an active investment approach that tries to improve the standard approach under modern portfolio theory. In particular, Treynor and Black propose an approach that ries to take into account investors’ security selection in the optimization process.
Treynor-Black model
Want to apply the Treynor-Black model yourself? Download our Excel file: Treynor Black Calculator.