Arbitrage pricing theory

In financial markets arbitrage are the forces taking place such that any present inefficiencies are exploited. As a result, securities will be prices correctly relatively towards each other. Suppose 1 euro is traded against 1.25 dollar in the US whereas 1 euro in Europe trades for 1.2 dollar. In this case, arbitrage takes place by selling dollar for euro in the US and buying dollars for euro in Europe until both prices are equal.

Portfolio valuation

Arbitrage pricing theory can also be used to value portfolios. In order to build an arbitrage portfolio, 4 conditions need to be fulfilled from which the last is often neglected.

  1. No investment
  2. No systematic risk exposure
  3. Positive payoff
  4. No unsystematic risk exposure

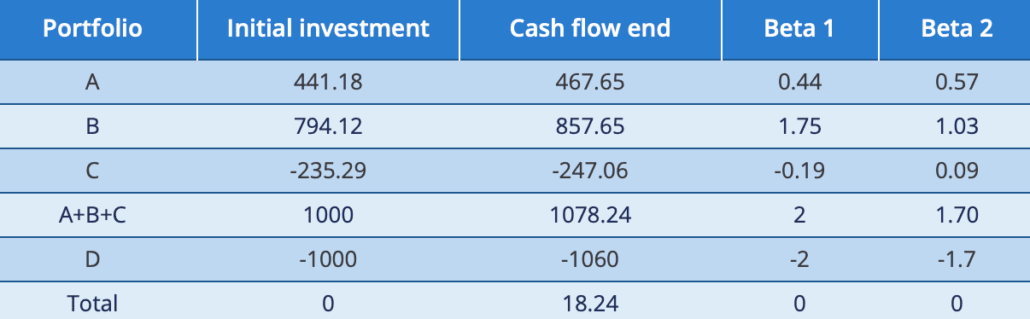
Suppose we have 3 well-diversified portfolios, meaning no unsystematic risk left, with the following risk-return profile and exposure to 2 risk-factors.

r_i = \alpha_i + \beta_{i,1} \cdot F_1 + \beta_{i,2} \cdot F_2

From this we can estimate the factor numbers and in turn determine whether the fourth portfolio is overvalued or undervalued

asset pricing theory inputs

The estimated constant equals 3.824, the first factor equals 1.667 and the second factor equals 0.392. From this we can determine that the required return on portfolio D should be equal to 7.824. In reality it is only 6, thus the security is overpriced and can be shorted.

By shorting portfolio D and investing a specific amount in the other portfolios, it is possible to construct an overall portfolio which is not exposed to any systematic risk. Moreover, it holds a positive return of 18.24 at the end of the investment period and didn’t require an initial investment.

asset pricing theory analysis

Equity valuation

In case of equity valuation, the same principles of arbitrage pricing theory can be applied. Based on common risk factors for multiple securities, these can be valued relatively towards each other. This in such a way that there is no net investment, a positive payoff and no systematic.

Unfortunately, there is unsystematic risk left but this does not affect pricing since this type of risk is not compensated. Although not important for pricing, it should be kept in mind for trading purposes. For example, pair trading is not arbitrage since either of the 2 companies might be affected by firm-specific (good or bad) news.

Summary

Arbitrage pricing theory values a security relatively towards others based on risk factors. The arbitrage forces in the market increase market efficiency and let free lunches vanish.