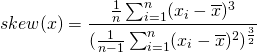Basic statistics

Measuring the return and risk of securities and portfolios is a crucial element of anyone active in finance. In order to do these calculations, it is necessary to master some key concepts in statistics. Below we explain some of the basic statistics needed in finance.

Mean

The estimated mean return of a security over a given period of time is a measure of the security’s expected return. It is calculated by taking the sum over the past realized returns (denoted x) and dividing this value by the number of observations (n).

$\overline{x} = \frac{1}{n}\sum_{i=1}^{n}x_i$

Variance and standard deviation

Standard deviation is the basic measure used to quantify the riskiness of a security. Standard deviation equals the square root of variance. The latter is measure of dispersion around the mean. To calculate the variance (s²) be, we use the following formula.

$s^2 = \frac{1}{n-1}\sum_{i=1}^{n}(x_i-\overline{x})^2$

Taking the square root of the above formula, we obtain the standard deviation (s).

$s = \sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(x_i-\overline{x})^2}$

Skewness

Skewness can be interpreted as an additional measure of risk. Skewness measures whether the distribution of realized returns is symmetric, negatively skewed, or positively skewed. In finance, when returns are negatively skewed, it means that there are more large negative returns than would be expected if returns are normally distributed. The more securities are negatively skewed, the higher the tail risk they are exposed to. This means that they are more likely to experience sudden large negative returns.

$skew(x) =\dfrac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\overline{x})^3}{(\frac{1}{n-1}\sum_{i=1}^{n}(x_i-\overline{x})^2)^\frac{3}{2}}$

Kurtosis

The kurtosis of a security can also be considered a measure of risk. Kurtosis measures the degree to which returns are close to the center of the distribution. In particular, the higher the kurtosis, the more returns are concentrated to the center. As such, a security with a high kurtosis shows little price movement most of the time. A high kurtosis indicates that large price changes have not occurred in the past. However, this does not mean that such sudden are not possible. Similarly, securities that have a low kurtosis will have experienced wider price changes in the past.

$kurt(x) = \dfrac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\overline{x})^4}{(\frac{1}{n}\sum_{i=1}^{n}(x_i-\overline{x})^2)^2}$

Correlation

In finance, (pearson) correlation measures the linear dependence between 2 assets. It plays a crucial role in modern portfolio theory, as explained in Markowitz portfolio selection. Correlation indicates how one asset is likely to behave if the other asset changes in value. Assets with positive correlation are likely to move in the same direction, both up or both down. In contrast, assets having a negative correlation move in opposite direction. If one asset move up, the other asset is likely to move down.

$\rho_{xy} = \dfrac{\sum_{i=1}^{n}(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{\sum_{i=1}^{n}(x_i-\overline{x})^2\cdot \sum_{i=1}^{n}(y_i-\overline{y})^2}}$

Summary

Return and risk measurement are very important. Mean, standard deviation, skewness,kurtosis and correlation are easy to calculate statistics based on a security’s past performance that hold a lot of information on the security’s return behaviour.