Portfolio optimizaton

Portfolio optimization refers to the process of selecting and weighting a portfolio of assets or investments to achieve a specific investment objective. Different investment objectives that investors can consider are:

Other more complicated portfolio optimization approach exist, such as minimum correlation, maximum diversification or hierarchical risk parity. The goal of any portfolio optimization technique is to carefully select and weight a portfolio of assets to achieve attractive risk-adjusted returns.

Most of the time portfolio optimization is used to determine the optimal risky portfolio or the mean-variance efficient portfolio.

This concept is related to the capital allocation line (CAL). The steeper the CAL, the more attractive a portfolios constructed from that CAL. This is because portfolios on a steeper CAL compensate the investor more for taking additional risk. They have a higher slope and thus Sharpe ratio. Modern portfolio theory can be used to determine the set of portfolios that provides the best risk/return trade-off for a given level of risk.

Mean-variance optimizaton in practice

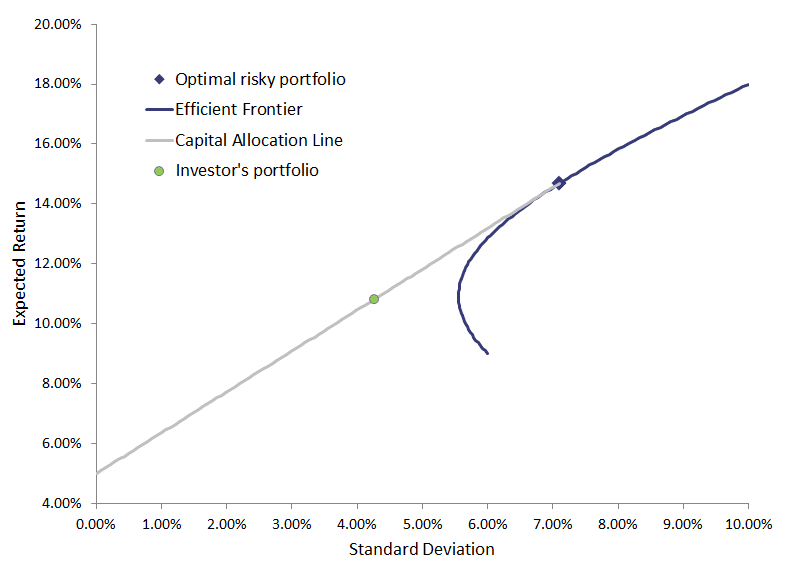
Portfolio optimization allows us to select the portfolio on the efficient frontier with the highest Sharpe ratio. This is where the capital allocation line is tangent (i.e. just touches) to the efficient frontier.  The figure below illustrates how we combine the CAL and the efficient frontier to determine the optimal risky portfolio.

PortfolioOptimization

This particular portfolio (highlighted here with a square) will serve as the risky asset in the investor’s overall portfolio.

Investors now still need to decide on how much of the portfolio to invest in the risky portfolio we just determined, and how much to invest in the riskfree asset.

This subjective decision depends on how much risk an investor is willing to take. For example, an investor could decide to invest 40% in the riskfree asset, and 60% in the optimal risky portfolio. This particular portfolio corresponds to the green dot on the capital allocation line.

Using Excel

The Excel file available on at the bottom of this page allows you to implement the entire portfolio optimization we just described above.

Limitations of portfolio optimization

There are some limitations tportfolio optimization:

  • First, we need to estimate a lot of variables to be able to optimize a portfolio. As an example, suppose we want to determine the optimal risky portfolio using mean-variance optimization. If we have 50 securities we want to include then we need to estimate 50 variances, 50 expected returns, and (502-50)/2 = 1125 covariances.
  • Second, the results of the portfolio optimization method proposed by Markowitz is very sensitive to the outputs. When expected returns, standard deviations, and covariances change slightly, the weights we obtain willy typically vary a lot.
  • Third, the weights we obtain are often extreme (so-called corner solutions). More often than not, the approach suggests we should allocate everything in just a hand full of shares.

These limitations lead some people to prefer alternative portfolio construction approaches we mentioned earlier in the introduction.

Summary

When we combine the capital allocation line and markowitz’s portfolio selection approach, we can perform portfolio optimization. This is just one optimization approach investors can choose from.