Representativeness heuristic
The representativeness heuristic is a cognitive bias that influences financial decision-making. Representativeness is the extent to which an event is representative of its parent population. A heuristic is a simple rule (‘shortcut’) used when making judgements. Heuristics are generally useful in that they make decision-making simpler. In particular, heuristics help us when we need to make decisions quickly. However, sometimes shortcuts send us off course.
Taking both elements together, the representativeness heuristic refers to the fact that we mentally take a shortcut by judging that something is more representative than it actually is. In particular, we judge the likelihood of an event simply based on how closely it resembles other events they are familiar with.
Representativeness Heuristic in Finance
Representativeness heuristics can lead investors astray. For example, investors might be tempted to forecast future earnings using the short histories of high earnings growth observed in the past. These estimates are then used to price the company’s stock and could thus lead to overpricing.
In this case, investors are failing to take into account the fact that the high earnings growth could just be due to chance. The high earnings growth is unlikely to repeat itself and might actually lead to disappointment. When future earnings are lower than forecasted, the stock price could drop considerably.
Another example that is very common is the fact that many investors avoid certain investments that are new or unfamiliar because they don’t fit their mental prototype of a “good investment.”
The representativeness heuristic may cause us to see patterns in data that are in fact random. Or we may think that future patterns will resemble past ones. This behaviour often occurs in finance when investors analyse charts of companies’ stock prices.
Investors search for patterns patterns or trends from which they can then benefit. However, often investors only identify trends when they are already well established. As such, investors are more likely to react to them, rather than that they are succesful in forecasting changes in these trends.
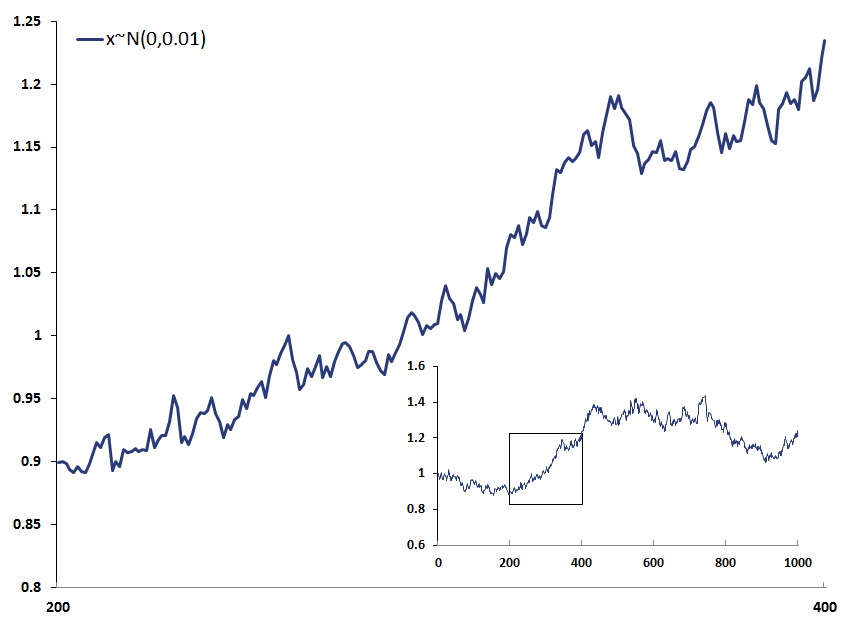
To illustrate our tendency to see patterns in random data, consider the following figure. If we only observe the magnified part of the chart, we might be tempted to assume that it is a continuously increasing series.
However, this is not the case. This particular series is actually part of a larger time series, as shown in the fiture. Clearly, the set of observations is not representative of the larger population.
The time series we plotted above is an example of a time series where changes are random and normally distributed, i.e. x~N(0,0.01). Like a fair coin, the time series is equally likely to go up or down.
Summary
A representativeness heuristic is often useful as is it makes decision-making easier. However, in finance it might cause us to draw wrong conclusions. For example, we might wrongly extrapolate the good recent performance of stocks.