Hyperbolic discounting
Hyperbolic discounting is a behavioural bias that’s basically an incorrect application of discounting cash flows. Hyperbolic discounting states that people prefer sooner payoffs to later payoffs in a way that’s irrational. If the payoff in the future is larger than the more immediate payoff, we opt for the more distant payoff depending on the ‘time gab’. However, these more distant payoffs get less weight than should be the case. In other words, we tend to incorrectly trade-off present and future tradeoffs.
Hyperbolic discounting is driven by temporal myopia. Temporal myopia causes clarity or our perception of the future to decrease with distance. And, rather than making us more conservative or more careful, this uncertainty makes us reduce the importance of the future in decision-making, i.e. hyperbolic discounting. Consequences which occur in the future, tend to be less important in decision-making, the more distantly they fall in the future.
Example
In finance, hyperbolic discounting is something quite tangible, as we can actually discount cash flows. Suppose someone offers you the choice between $50 right now, or $100 tomorrow. In this case, waiting until to tomorrow is a small price to pay to receive twice as much money. However, as the ‘delay gap’ widens, the value of the additional amount of money decreases. Suppose you can choose between $50 now a $100 in one year, would you still opt for the larger payoff?
The pattern that emerges from the way people choose as time increases, follows a hyperbola. Suppose we have to wait for 2 years before we get the $100. Far more people will decide to go for the immediate payoff when they have to wait two years, rather than one. Very few people will want to wait two years.
Another example where hyperbolic discounting is at play in finance is when people borrow money, either through loans or credit cards. When borrowing money, people spend future resources to consume more today. This means that they have high discount rates, and value current consumption a lot more than future consumption.
Consider a third example. Suppose you can choose between 2 ETFs to invest in. The first capitalizes the earnings from its investment. The second however, pays a dividend to shareholders., e.g. next month. There are no other differences between these 2 ETFs and there are no taxes to be paid (no dividends nor capital’s gain tax). Investors prone to hyperbolic discounting prefer investing in the second ETFs, since it generates a gain in the near future.
Mathematically
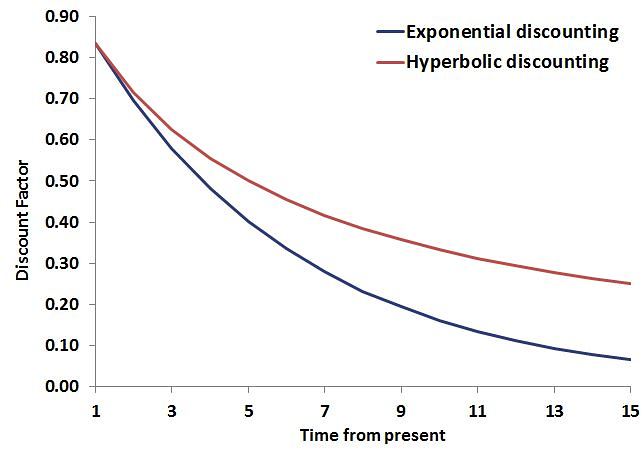
In principle, we should discount the value of the future reward, by a factor that increases with the length of the delay. As such, we should use exponential discounting, which is a time-consistent way of discounting. However, research found that people don’t seem to be using a constant discount rate.
Let’s consider the following example to walk us through the irrational behaviour that is captured by hyperbolic discounting. If we want to rationally discount a future reward E, we would use the following formula
where r is the discount rate, B is the present value, and t is time (expressed in years). If the present value of the future reward E exceeds the value of the present reward, we should select the future reward.
Instead, someone who performs hyperbolic discounting, makes a logical error when discounting. For example, that person might be using the following formula
t again captures the delay in the reward, and r is the discount rate. In both cases, a high discount rate means that we value current consumption considerably more than more consumption in the distant future. However, if we use hyperbolic discounting, we discount the distant reward too much.
Summary
Hyperbolic discounting is the tendency for being short sided and therefore adjusting our behavior accordingly. By being aware of this tendency to perform hyperbolic discounting, we can account for the effect and more consciously make decisions that have future consequences.