Interest Rate Swap Valuation

Interest rate swap (IRS) valuation is very simple. Valuing an interest rate swap only requires the discount factors that are based on the LIBOR curve. Using these discount factors, we can calculate the swap fixed rate, which is the price of the interest rate swap.

But before we continue, let’s briefly discuss the definition of an interest rate swap. In an interest rate swap, one party agrees to pay floating and receive fixed. At the start of the swap, the fixed rate is calculated such that the present value of the floating-rate payments is equal to the present value of the fixed rate payments. If that is the case, then the value of the swap is zero to both parties. The fixed rate determined this way is the swap rate.

Interest rate swap fixed rate

Let’s compute the swap fixed rate. The rate is derived from the LIBOR curve corresponding to the swap tenor. Suppose we wish to create a two-year swap that settles twice a year. In that case, the LIBOR rates we need are the rates corresponding to the four settlement dates of the swap.

If we have these four rates, we should first calculate the discount factors using the following formula

    $$ = \frac{1}{(1+(LIBOR \cdot \frac{days}{360}))} $$

Note that we are using a 360 days convention.

Once we have the discount factors, we can calculate the periodic swap fixed rate (SFR) as

    $$ \textrm{SFR(periodic)} = \frac{1- \textrm{final discount factor}}{\textrm{sum of discount factors}}$$

To annualize this rate, we use the following formula

    $$\textrm{swap fixed rate (annual)} = \textrm{SFR(periodic)} \cdot \textrm{\#settl. periods p.a.} $$

Interest rate swap valuation

As short-term interest rates change over the life of the swap, its value will fluctuate. It will be positive to one of the parties, and negative to the other. In particular, if interest rates go up, the swap will have a positive value to the fixed-rate payer. Similarly, if interest rates go down, the floating-rate payer will make a profit.

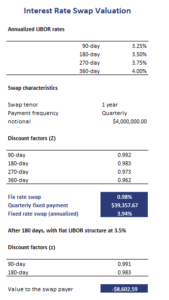
Let’s apply the above formulas to determine the swap fixed rate. The following table implements an example. The spreadsheet is available for download at the bottom of the page. In addition to pricing the swap, we also value the interest rate swap.

Interest-Rate-Swap-Valuation

The formula we need to use to value the swap on settlement dates is

    $$ \textrm{value to the payer} = \sum Z \cdot (SFR_{new} - SFR_{old}) \cdot \frac{days}{360} \cdot \textrm{notional} $$

where days is the number of days in the settlement period.

Summary

We discussed the pricing and valuation of interest rate swaps. Once we know the discount factors, pricing a swap is a matter of simply applying the formula.