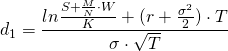Warrant valuation

Warrants are a peculiar type of derivative that behave like an option. Unlike options, warrants are issued by a company in order to attract funding, or increase the attractiveness of order issued securities, for example bonds. This has the consequence that when warrants are exercises (call), the company’s equity goes up resulting in dilution.

Warrant valuation ingredients

As a starter, suppose a company has N shares outstanding representing for a value V. Moreover, the company has also issued M warrants, each of them entitled to buy g shares for a price K. When all warrants are exercises, the share price will, as a result of dilution be equal to the value of the firm before exercise (V) plus new equity (MgK), divided by the sum of outstanding shares (N) plus newly issued shares (Mg).

P_{after} = \dfrac{V + M \cdot g \cdot K}{N+M \cdot g}

The warrantholder thus gets a payoff:

Payoff = max(g\cdot (P_{after}-K),0)

Which can be rewritten as a number of calls on V/N

Payoff = \dfrac{N \cdot g}{N+M \cdot g} \cdot max(\dfrac{V}{N}-K,0)

Warrant valuation formula

Warrant valuation requires the Black Scholes formula to be accommodated for dilution. This can be done by determining the amount of outstanding shares, issued warrant, and the entitled amount of shares. Note that the volatility in the adjusted model both needs to be adjusted to both measure the variability from stocks and warrants.

W_{european} = ((S + \dfrac{M}{N} \cdot W) \cdot N(d_1) - K \cdot e^{-r \cdot t} \cdot N(d_2)) \cdot \dfrac{N \cdot g}{N+M \cdot g}

With

d_1 = \dfrac{ln{\frac{S + \frac{M}{N} \cdot W}{K}}+(r+\frac{\sigma^2}{2})\cdot T}{\sigma \cdot \sqrt{T}}

d_2 = d_1 - \sigma \cdot \sqrt{T}

Since W, is both on the left and right hand side of the equation, it is not possible to do warrant valuation analytically. They have to be valued numerically.

Summary

Warrants entitle the holder the right to buy or sell an asset at a certain price in the future. When exercised, the company issued new shares (call) which results in dilution. Due to their nature, warrants valuation based on option pricing requires a dilution adjustment.