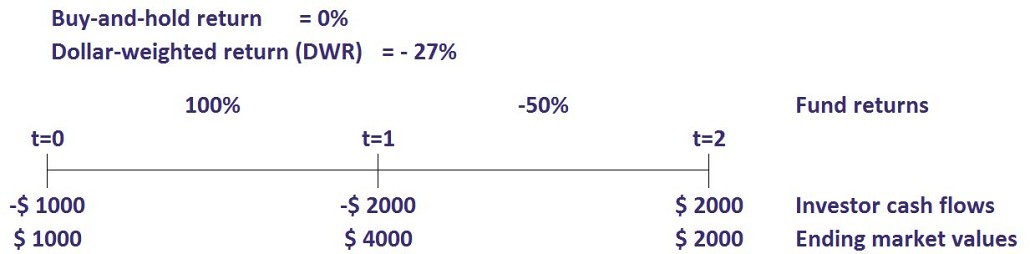Dollar-weighted return (DWR)

The dollar-weighted return (DWR) measures the rate of return of an investment or a portfolio, taking into account the timing of flows. It is defined as

the rate of return that equates the discounted ending asset value to the sum of the initial assets-under-management and the present value of the capital flows realized over the life of the investment.

Dollar-weighted rates of return (DWRR) differ from the more commonly used time-weighted rate of returns (TWRR) in that dollar-weighted returns take into account an investor’s ‘behavior’. This is because the dollar-weighted return reflects the impact of flows on performance. In addition, dollar-weighted returns will more accurately reflect the actual growth rate of an investment or portfolio.

The above dollar-weighted return definition probably sounds somewhat abstract. Therefore, we will first provide the formula needed to calculate dollar-weighted returns and illustrate it using a numerical example. In addition, we also provide a simple Excel spreadsheet that allows you to calculate the dollar-weighted return of an investment yourself.

Dollar-weighted return formula

The formula needed to calculate the dollar-weighted rate of return is

\dfrac{\textrm{AUM}_t}{(1+r_{dw})^t} = \textrm{AUM}_0 + \sum_{t=1}^{T} \cfrac{\textrm{Capital flow}_t}{(1+r_{dw})^t}

where rdw is the dollar-weighted return, AUM0 is the initial investment, Capital Flowst are the flows in and out of the investment, and T is time (in years). Basically, calculation of dollar-weighted returns amounts to ‘weighting’ the different capital- or ‘money’ flows in and out of the portfolio. That’s why this type of return is sometimes also referred to as the money-weighted return (MWR) or the money-weighted rate of return (MWRR).

To solve the above equation, we should therefore solve for the unknown rdw. In particular, we need to determine the rate of return that equates the left-hand side and right-hand side of  the above equation. This calculation is basically an internal rate of return calculation that can be be performed using simple spreadsheet software.

Dollar-weighted rate of return example

Let’s consider a numerical example that shows the usefulness of calculating dollar-weighted returns. In particular, let’s compare the money-weighted rate of return and the time-weighted return of an investment.

Let’s consider a small investor that buys 100 shares of the fund AlphaFund at $10 per share at time 0. Hence, his initial investment is $1000. Next, lest assume that the realized returns over the first period is 100%. At the end of time 1, the investor’s investment is worth $2000. Because of the good performance the investor decides to buy another 100 shares. Hence, he invests an additional $2000 in AlphaFund. Unfortunately, the performance in the second period is bad. The fund loses 50% of its value. Because of the bad performance, the investor decides to liquidate the fund.

Over this period, the time-weighted-return is 0%. The investor’s return experience, however, is negative. He invested $3000 in total, but only got $2000 when liquidating his position. Applying the above formula to the provided data

\dfrac{2000}{(1+r_{dw})^2}= \dfrac{1000}{(1+r_{dw})^0} + \dfrac{2000}{(1+r_{dw})^1}

we find that dwr should equal -26.7% for the left-hand side to equal the right-hand side. The following figure illustrates the investor’s return experience.

dollar-weighted-return-bad-timing

bad timing

Of course, the opposite case is also possible. Suppose the fund initially underperformed and it lost 50% of its value. Despite the bad performance, the investor decides to buy additional shares in Alphafund. In particular, he also invests $2000 at the end of time 1. The fund subsequently recovers and the investor again decides to liquidate the fund.

In this case, even though the time-weighted return of the fund is the same, the investor’s return experience is markedly different. In particular, the investor realizes a 45% gain.

dollar-weighted-rate-of-return-good-timing

good timing

In the spreadsheet below we further illustrate how to perform a money-weighted rate of return calculation. We show this using the above formula as well as a built-in formula in Excel. The built-in function is called XIRR and allows you to calculate internal rates of return.

Summary

Money-weighted returns better capture the return experience of investors. They capture the impact of capital flows on an investment’s performance.

Dollar-weighted return calculator

Want to calculate the dollar weighted average return yourself? Download our Excel spreadsheet: dollar-weighted-return