Minimum variance portfolio 

The minimum variance portfolio or minimum risk portfolio is a so-called risk-based approach to portfolio construction. This means that, instead of using both risk and return information as in the Markowitz portfolio selection, the portfolio is constructed using only measures of risk. One reason why investors might want to opt for a risk-based approach, is the fact that expected or future returns are very hard to estimate. Risk, however, is easier to estimate. This leads to a more robust portfolio that is less subject to estimation risk.

On this page, we explain the relationship between the minimum variance portfolio and the efficient frontier, provide formulas to determine the minimum variance portfolio weights, and provide and Excel sheet that implements the approach.

Global minimum variance portfolio

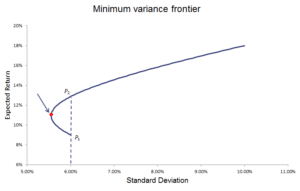
The min variance portfolio is related to modern portfolio theory and the efficient frontier. In particular, it is a unique portfolio that is on the efficient frontier. In the following figure, we highlight the min variance portfolio using the red dot. It is clear from the figure that the portfolio with the lowest standard deviation that can be constructed from the set of securities that the investor  can invest in. To construct the efficient frontier, there’s an Excel file on the page portfolio optimization.

minimum variance portfolio

Minimum variance portfolio formula

To calculate the minimum variance portfolio weights, we can make use of the following minimum variance portfolio formula. To do this, all we need is the covariance matrix \Sigma. It is important to note that we do not need the expected returns to determine the weights.

The weights w_{MV} = (w_{MV,i},...,w_{MV,N})'  of the min variance portfolio are given as

    $$w_{MV} = \frac{\Sigma^{-1}\mathb{1}}{\mathbf{1}\Sigma^{-1} \mathbf{1}}$$

where \mathbf{1} is a column vector of ones. The expected returns of the portfolio can be calculated as

    $$\mu_{MV} = \mu' w_{MV} = \frac{\mu' \Sigma^{-1}\mathbf{1}}{\mathbf{1}\Sigma^{-1}\mathbf{1}} $$

where \mu is the vector of expected returns. The portfolio minimum variance equals

    $$ \sigma_{MV} = w'_{MV} = \frac{\mathbf{1}}{\mathbf{1}\Sigma^{-1}\mathbf{1}}$$

Minimum variance portfolio calculator

The above formulas provide a closed-form solution to calculate the global minimum variance portfolio. It can easily be calculated using software that allows for matrix algebra. In Excel, we can also calculate the global min var portfolio using Excel’s Solver. In the Excel file below, we apply this approach to come up with a minimum variance portfolio calculator.

Global minimum variance

Want to have calculate the global min variance portfolio using Excel’s solver? Download the Excel file: Minimum Variance Portfolio