Equal volatility weighting
Equal-volatility weighting, or EV, is a risk-based asset allocation approach that is closely related to risk-parity. It is sometimes also referred to as inverse volatility weighting. On this page, we discuss the concept of equal-volatility weighting, provide a simple example, and provide a simple Excel implementation of how to determine the equal vol weights.
Definition equal volatility weighting
Equal-volatility weighting, sometimes also referred to by institutional investors as ‘equal-vol weighting’ or EV, is a risk-based weighting approach that is quite different from market capitalization weighting. Rather than allocating capital based on the companies’ market capitalization, as is the case for the S&P 500 index, equal-vol weighting will weight all the securities based on the riskiness.
In particular, if a security is more risky, the equal-volatility approach will assign less weight to it. Similarly, if the security is not very risk or volatile (e.g. a government bond) the strategy will assign more weight to position. More specifically, the equal volatility approach will allocate such that the contribution of every position to overall risk is the same.
Equal-volatility formula
The formula needed to perform an equal-risk weighting approach is the following. Let’s consider two assets with ![]() and
and ![]() . In that case, the weights will be
. In that case, the weights will be
![]()
for security A and
for security B.
Numerical example equal-volatility approach
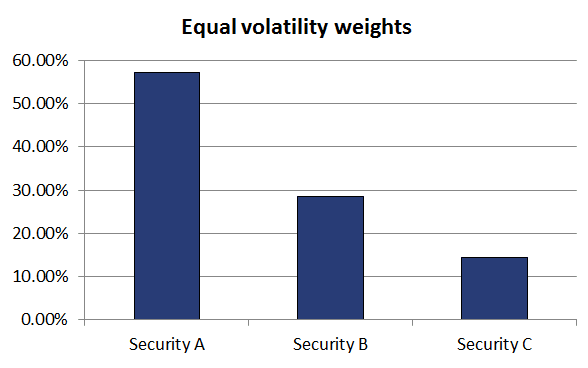
Let’s consider an example with three assets. The first asset (security A) has a volatility of 5% per year, the second security (security B) as a volatility of 10%, and the third security (security C) has a volatility of 20% per year. In that case, the weights are
for security A.
for security B.
for security C.
This shows that the securities are weighted by using the inverse volatility. A simple implementation of the equal volatility approach for more than two assets can be found in the Excel file at the bottom of the page.
Disadvantages equal-volatility weighting
There are also downsides to using an equal-volatility approach. In particular if the volatility of a security is unusually low, we assign a large weight to it. If, however, the volatility goes back to its normal level, then you may have a too big weight in the security.
Another problem with the EV approach is that we do not take into consideration correlations. This is the case when you consider a risk parity approach. This is why the EV approach is sometimes referred to as naïve risk parity.
Summary
We have discussed the concept of equal-vol weighting or inverse volatility weighting. Equal volatility weighting is an approach that has received considerable attention in recent years. It will allocate capital to different positions based on the riskiness of the securities. It does not, like the modern portfolio approach, consider expected returns. The EV approach is easily implemented in Excel, as is illustrated in the .xlsx below.
EV calculation
Want to have an implementation in Excel? Download the Excel file: Equal volatility weighting.