Prospect theory
Prospect theory is a theory of decision-making under risk. The theory was first proposed at the end of the 1970s by Daniel Kahneman and Amos Tversky. Prospect theory goes against some of the fundamental assumptions that underly modern finance. In particular, it challenges another decision-making theory called the “expected utility theory“.
Expected utility theory is a set of assumptions made in economics on how humans are expected to behave under uncertainty. Amongst other things, expected utility theory states that people correctly assess probabilities and that they experience good things and bad things equally.
Although prospect theory also has a lot to say about some of the other assumptions that underlay expected utility theory, the above two are the most important. Psychological tests have shown that humans are bad at assessing probabilities (see the base rate neglect, sample size neglect, gambler’s fallacy) and that they find bad things relatively worse than they find good things (see loss aversion, disposition effect).
Editing and evaluation phase
Prospect theory agues that people go through two distinct stages when comparing choices under uncertainty. First, there is the editing phase. During this phase, people are said to compare the different ‘prospects‘. To do this, they edit the complicated decisions they have to make into simpler decisions, specified in terms of gains versus losses.
For example, purchasing a lottery ticked is simplified into losing $1 and gaining a small chance to win $1million. This is called ‘coding’. During this editing phase, people also several other methods to determine whether outcomes can be ignored (outcomes that are ‘dominated’), outcomes that are riskless (‘segregating’ the outcomes), etc.
In the second phase, the evaluation phase, people examine the edited prospects and then choose the one with the highest value. This choice is based on two dimensions, the apparent value of each outcome, and the weight (similar to the objective likelihood, although not identical).
Value and weighting function
The choice between the different outcomes is determined by combining an outcome’s apparent value, predicted by the value function, and the importance or weight that people assign to the particular outcome, i.e. the weighting function.
Value function
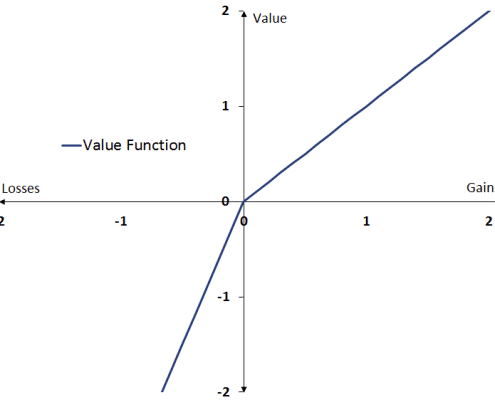
The value function has three critical aspects
- value is assigned to changes in value rather than absolute value
- the value function is S-shaped (see figure) and is expected to be concave for gains above the reference point, but convex for losses below the reference point
- the value function is steeper for losses than for gains (see figure)
In the second phase, the evaluation phase, people examine the edited prospects and then choose the one with the highest value. This choice is based on two dimensions, the apparent value of each outcome, and the weight (similar to the objective likelihood, although not identical).
Value and weighting function
The choice between the different outcomes is determined by combining an outcome’s apparent value, predicted by the value function, and the importance or weight that people assign to the particular outcome, i.e. the weighting function.
Value function
The value function has three critical aspects
- value is assigned to changes in value rather than absolute value
- the value function is S-shaped (see figure) and is expected to be concave for gains above the reference point, but convex for losses below the reference point
- the value function is steeper for losses than for gains (see figure)
As for the first aspect, prospect theory predicts that the value of different prospects is determined only by comparing it with the other options. Hence, the value people assign to an outcome depends on the other outcomes that people are comparing it with.
This comparison is called a reference point. Hence, a trip to Europe might sound wonderful when compared to a trip to a neighbouring state. However, it doesn’t sound nearly as wonderful when compared to a trip to the Fiji.
Hence, the value of the object under consideration (‘the trip to Europe’) is determined by the change in value between the object (‘the trip to Europe’) and the reference point (‘the next town’ or ‘Fiji’), and not the absolute value of the object (‘the trip to Europe’ itself). As a consequence, people will reject the same option in different situations.
The concave shape of the value function implies that small changes around the reference point are assigned a high value, whereas bigger changes are assigned smaller values. For example, the difference between winning $10 an $5 leads to a large change in the value, but winning $1000 or $1005 has little impact. Even though the size of the change is the same (i.e. $5).
Finally, the asymmetric shape of the value function captures the fact that people are loss averse. This means that a loss is assigned a greater value than a gain of the same amount.
For example, losing $10 feels worse than winning $10 feels good. It also implies that people will be risk-seeking in the domain of losses, but risk-averse in the domain of gains. People will take more risk to avoid a loss (to avoid falling short) than to ensure a gain.
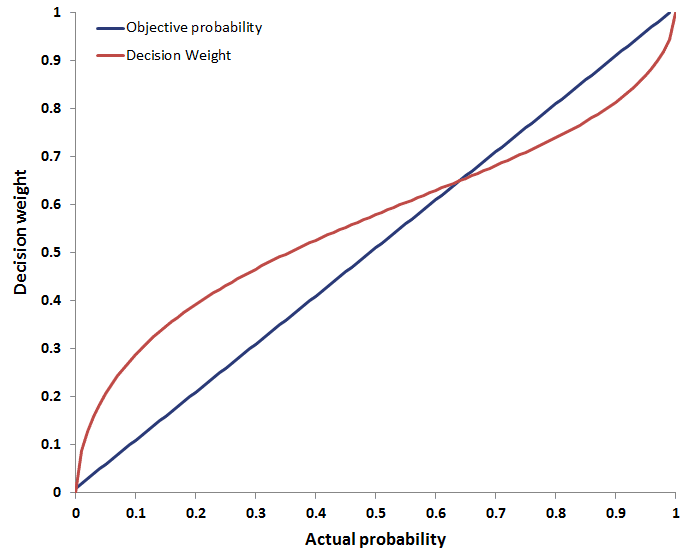
Weighting function
The weighting function is an alternative weighting scheme to the one used under the expected utility theory. Under the latter theory, the objective likelihood that an outcome will occur is used to weigh the different outcomes.
Under prospect theory, we assume that people multiply the perceived outcome by a decision weight. These decision weights differ from the objective probabilities in the case of extreme probabilities.
For example, moving from having no chance to contracting an illness to having a 1% chance of contracting it, will have a much larger effect on one’s decision-making than moving from a 50% to a 51% chance. Even though the increase in likelihood is identical (1%), the increase in the decision weight will be larger. People tend to overweight low-probability events.
Summary
Prospect theory tries to explain how people make decisions under uncertainty. A lot of the behavioral biases we will discuss further on, can be explained using this framework.