Sample Size Neglect
Sample size neglect, sometimes also referred to as the ‘law of small numbers‘, is an example of a bias caused when we rely on representativeness heuristics. In this case, when we have to judge the likelihood that a set of observations was generated by a particular model, we often fail to take into account the size of the sample.
Sample Size Neglect Example
It is true that a small sample of observations, e.g. six tosses of a coin resulting in three heads and three tails, can be just as representative of a fair coin as a large sample of observations (500 heads and 500 tails). However, the second sample is more informative. Still, we tend to find both samples equally informative about the fairness of the coin.
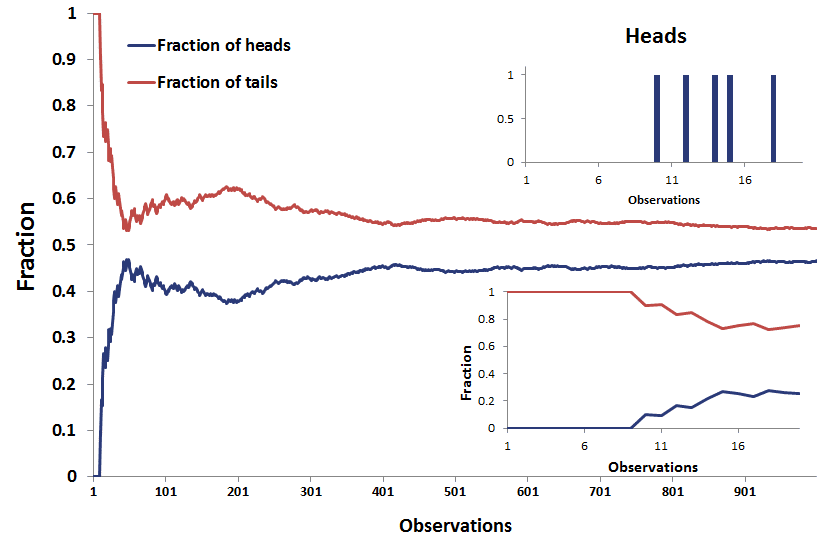
The following figure, using Excel, illustrates the importance of sufficiently large samples. In Excel, we simulate tossing a fair coin. Even though the coin is fair, only 5 out the first 20 observations are heads. While the fraction of heads and tails should (and will) converge to 50%, this happens only slowly. Even after a 1000 observations, convergence is still not the case. Clearly, we need a lot of observations before we can conclude whether a coin is indeed fair.
Sample size neglect suggests that, when we don’t know the ‘data generating process’, we will infer it too quickly on the basis of too few observations.
Sample Size Neglect In Finance
Investors are confronted with small samples all the time. For example, you might believe a financial analyst to be skillful if he has 5 consecutive good stock picks. However, 5 successes is too small to be able to judge whether the analyst is truly talented or whether it is due to luck.
Similarly, we shouldn’t jump to conclusions when evaluating mutual fund managers’ track record. Even if the track record spans several years, the size of this ‘sample’ is typically not long enough to determine whether the fund manager is truly skilled.
Related biases
In cases where we do know the ‘data generating process’, the law of small numbers is called the gambler’s fallacy.
Summary
We discussed sample size neglect, the tendency for investors and analysts to draw conclusions based on a small sample size of data, without considering the statistical significance of their findings.
Sample size neglect is a very important consideration when dealing with financial data. A fairly large data set, covering several years, can still be unrepresentative of the data generating process of a strategy.