Fixed Income Forward Valuation
Fixed income forward valuation is used to price and value forwards on fixed income securities. Pricing of fixed income forwards is typically based on the condition that arbitrage is not possible.
On this page, we show that pricing a fixed income forward is remarkably similar to pricing a dividend paying stock. Once the price is set, the value of the forward contract will fluctuate. Thus, we should also be able to value the contract over time. For that purpose, we also discuss the formula to value a fixed income forward. Finally, we implement the above formulas such that all the methods become clear. The file used to implement the model is available at the bottom of the page.
Fixed income forward pricing
Let’s start by discussing the formula to price a fixed income forward. The formula is
or
where S0 is the current price of the bond, PVC (FVC) is the present value (future value) of the coupon payments over the life of the forward, Rf is the risk-free rate and T is the life of the forward contract.
Fixed income forward valuation formula
Next, let’s value the contract prior to expiration
where PVCt is the present value of the remaining coupon payments. We can also use different formula if we are given the current forward price on a fixed income forward on the same underlying bond and with the same remaining maturity.
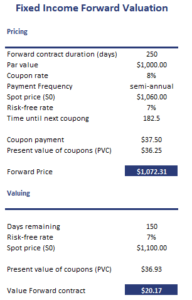
Fixed income forward valuation example
Next, let’s apply the above formulas using a simple numerical example. The table below calculates both the price and the value of the same fixed income forward contract.
The spreadsheet used to create the example is available for download below.
Summary
We discussed how to price and value fixed income forwards. The formulas are identical to the formulas used to value a dividend-paying stock.
Download the Excel spreadsheet
Want to have an implementation in Excel? Download the Excel file: Fixed Income Forward Valuation template