Valuation Capped Floater

A floating rate bond (a floater) is a bond that pays a coupon that adjusts every period based on a reference rate. Popular reference rates used are the EURIBOR and the LIBOR. The coupon is typically determined at the start of each period, and paid in arrears (that is, at the end of each period). There are two types of floaters that are typically used; floored floaters and capped floaters.

On this page, we discuss how to value a capped floater and a floored floater. We also implement a simple capped floater example in Excel to illustrate the necessary methods. 

Capped floater formula

Let’s start by discussing the capped floater definition. A capped floater is a floating rate bond that includes an issuer option that prevents the coupon rate from rising above a certain maximum rate known as the cap. The formula equals

    $$\textrm{value capped floater} = \textrm{straight floater} - \textrm{value embedded cap} $$

Floored floater formula

The floored floater definition is the following. It is a floating rate bond that has a coupon rate that cannot fall below a specified minimum rate known as the floor. Thus, the owner of the bond is long an embedded option that offers protection against falling interest rates. The floored floater formula equals

    $$\textrm{value floored floater} = \textrm{straight floater} + \textrm{value embedded floor} $$

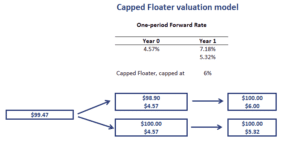
Capped floater valuation

We can value both capped floaters and floored floaters using the standard backward induction method in a binomial interest rate tree. At each node, we simply adjust the value of the floater to reflect the impact of the cap or floor. The following capped floater valuation example illustrates how the approach works.

Capped-Floater-Valuation-Model

The example illustrates that we simply have to adjust the interest paid at each node using the appropriate interest rate.

Summary

We discussed the valuation of floating rate bonds that have embedded options that protect the issuer (investor) against rising (declining) interest rates. Capped and floored floaters can easily be valued using the standard backward induction methodology that is used to value bonds with embedded options.

The above topic is related to the following set of topics:

  1. Bonds
  2. Bond valuation
  3. Fixed rate bond valuation
  4. Floating rate bond valuation
  5. Equity valuation