Singer-Terhaar Model
The Singer-Terhaar model is a financial equilibrium model that uses two versions of the international capital asset pricing model (ICAPM). In one of the ICAPM models global assets markets are fully integrated, and in the other markets are fully segmented. The model then looks at the expectations of actual segmentation/integration and takes a weighted average of the two assumptions to calculate returns.
On this page, we discuss the Singer-Terhaar model in detail. The process consists of 4 steps and it starts from the CAPM model. For more details on the CAPM, see the page on the capital asset pricing model. We also discuss an implementation of the model in Excel. The template can be downloaded at the bottom of the page.
Singer-terhaar model steps
Step 1:
The first step is to calculate the following beta
where rho is the correlation between the returns on asset i and the global market portfolio, sigma_i is the standard deviation of the returns on asset i, sigma_M is the standard deviation of the returns on the global market portfolio and Cov(Ri,RM) is the covariance of asset i’s returns with the global market portfolio return.
Step 2:
We rearrange the CAPM formula to arrive at the expression for the risk premium for asset i, RPi:
This expression states that the risk premium for an asset is equal to the product of its correlation with the global market portfolio and the standard deviation of the asset, multiplied by the Sharpe ratio for the global portfolio. Using this formula, we can forecast the risk premium and expected return for a market.
The Singer-Terhaar model then adjusts the CAPM for market imperfections, such as segmentation.
- When markets are segmented, capital does not flow freely across borders
- In the case of integrated markets, capital does flow freely.
If markets are segmented, two assets with the same risk can have different expected returns because capital cannot flow to the higher return asset. The more investment barriers, the higher the risk premium for securities in segmented markets.
In practice, markets are not fully integrated and not fully segmented either. As a rule of thumb, developed markets tend to be between 75% and 90% integrated. Emerging markets tend to be between 50% and 75% integrated. An important component of the Singer-Terhaar model is the estimation of the market integration parameter.
In the case of full segmentation, the relevant global portfolio is the individual assets as its own market portfolio, meaning that the asset is perfectly correlated with itself.
Step 3
Calculate the risk premium for asset i assuming a fully segmented market
Step 4
The last piece is to take a weighted average of the two risk premiums to calculate the asset’s risk premium
where G and S stand for globally integrated and segmented, respectively. Gamma is the market integration parameter.
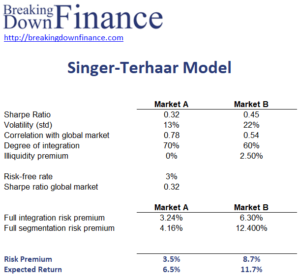
Tinger-Terhaar example
Next, let’s look at an example. The following table implements an example. The Excel spreadsheet can be downloaded at the bottom of the page
Summary
We discussed the Singer-Terhaar model, which can be used to calculate the equity risk premium for markets that are not completely integrated.
Download the Excel spreadsheet
Want to have an implementation in Excel? Download the Excel file: Singer-Terhaar Model Example