Cash Equitization

Cash equitization refers to purchasing index futures to replicate the returns that would have been earned by investing the cash in an index with risk and return characteristics similar to those of the portfolio. Cash equitization is also known as cash securitization or cash overlay.

On this page, we discuss the rationale behind a cash overlay and how to determine the number of contracts needed to perform a cash overlay. In particular, we discuss the cash equitization formula and implement the approach using an Excel spreadsheet. The approach borrows from the target portfolio beta approach.

Cash equitization methods

Holding cash balances will typically reduce the return of a portfolio because cash typically yields a lower rate of returns than equity or fixed income. Holding cash balances will therefore increase the risk that the portfolios will underperform the benchmark. Cash securization eliminates this risk. 

There’s at least two ways in which we can perform a cash equitization:

  • using futures contracts; these are liquid and have low transaction costs
  • using call and put options: buy call and sell put options on the appropriate stock index with the same strike and expiry to create a synthetic forward position

Next, let’s discuss the formula we can use to perform a cash overlay.

Cash equitization formula

The number of contracts needed to perform a cash overlay

    $$ \textrm{number of futures contracts} = \frac{\beta_{T} - \beta_{P}}{\beta_{F}}\cdot \frac{MV_{P}}{F} $$

where beta_T is the target portfolio beta, beta_P is the current portfolio beta, beta_F is the futures beta (beta of the stock index), MV_P is the market value of the portfolio, and F is het futures contract value (i.e. futures price times multiplier). In this case MV_P is the value of the cash position.

Since the current portfolio beta of the cash is zero we can simplify the formula as follows

    $$ \textrm{number of futures contracts} = \frac{\beta_{T}}{\beta_{F}}\cdot \frac{MV_{P}}{F} $$

Also, the target beta equals 1, since we simply want the beta of the synthetically invested cash to match the beta of the index.

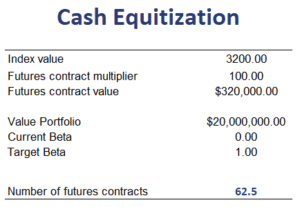
Cash equitization example

Let’s apply the above formula using a numerical example. The following table illustrates the approach. The spreadsheet used can be downloaded at the bottom of the page.

Cash Equitization

Summary

We discussed cash securitization or cash overlay, a method to the drag of cash in an equity portfolio.