Downside Deviation
Downside Deviation (DD) is a measure of risk that tries to address several shortcomings of standard deviation. Unlike standard deviation, downside deviation only considers the kind of volatility that investors dislike. That is, the volatility associated with negative returns.
On this page, we discuss the DD formula and definition as well as a numerical example. A downside deviation spreadsheet example is available for download at the bottom of this page.
Downside deviation definition
As the name suggests, DD only considers volatility in a security’s returns that is below a certain threshold. The threshold is called the Minimum Acceptable Return or MAR. DD was first proposed by Sortino and Price in 1994 in a paper called “Performance Measurement in a Downside Risk Framework” and it is part of the family of semi-deviation measures of risk.
Downside deviation formula
Since DD is simply the deviation vis-à-vis a certain threshold return, the formula is very straightforward. First define Lt
![]()
Then, downside deviation (DD) is defined as
for a given level of MAR. DD is strongly related to the Sortino ratio. This measure is similar to the Sharpe ratio, but uses DD in the denominator.
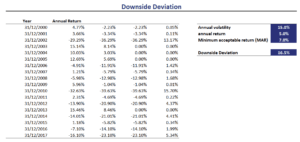
Downside deviation example
Let’s turn to example to get a better understanding of how we can easily implement this measure using a spreadsheet. The following figure illustrates the steps needed to calculate DD for a series of returns.
Advantages and disadvantages
While DD has some advantages, there are also disadvantages when using this measure. The first disadvantage is that in a lot of cases, standard deviation will yield similar results as downside deviation. The advantage of using the standard deviation, however, is that standard deviation is more well-behaved as a measure, whereas downside deviation can sometimes be hard to work with. Portfolio optimization using DD, for example, is generally not possible.
The main advantage of DD is that is a better measure of risk for investors that care about the downside risk in an investment. Investors who want to avoid drawdowns at all costs, can benefit from calculating DD.
Summary
We discussed DD, a measure of downside risk that is commonly used by investors that wish to avoid drawdowns. The DD measure is used by investors who wish to evaluate hedge funds and other types of absolute return funds. Several performance measures, such as the Sortino Ratio are calculated using DD.
DD calculator
A downside deviation calculator in Excel is available for download here: Downside Deviation template