Market-adjusted cost
The market-adjusted cost of a trade is a metric used to evaluate trade execution. Trade cost analysis is vital to assess the effectiveness of brokers, algorithms, and other strategies. Trade costs are typically expressed in basis point of the original benchmark price. The benchmark price could be the arrival price, VWAP, TWAP, or the closing market price.
On this page, we discuss the formula for the trade cost in basis points and show how to arrive at the market adjusted cost of the trade formula.
Trade cost definition
Let’s first start with the formula for the trade cost in basis points
There is a problem with using trade cost to evaluate trade execution. Buy orders in a rising market and sell orders in a falling market incur positive trading costs due to adverse price movements. We need to remove this impact of market movements on trade cost. This is done using the market-adjusted cost. But before we can calculate this cost, we first need to calculate the index cost. The index cost is a representation of the costs due to general market index movements:
Market-adjusted cost definition
The market-adjusted cost formula is the following:
where arrival cost is the arrival cost of the trade based on an arrival price benchmark and beta is the beta of the security versus the index used to calculate index cost.
Example
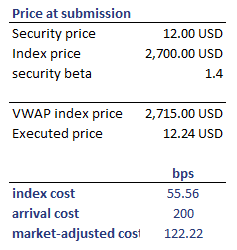
Let’s illustrate with an example. The following table illustrates the necessary steps. The spreadsheet used can be downloaded at the bottom of the page
Summary
We discussed the market-adjusted cost, which corrects the trade cost for the fact that the impact of general market movements should be removed during trade execution evaluation.
Download the Excel spreadsheet
Want to have an implementation in Excel? Download the Excel file: Market-adjusted cost calculator