Ho-Lee Model
The Ho-Lee interest rate model is a short-term interest rate model that is used to price derivatives on fixed income securities. The interest rate model was developed by Thomas Ho and Bin Lee in 1986. An important feature of this model is that interest rates can be negative. That’s because the model generates a symmetrical distribution (normal) of future interest rates. Another point to keep in mind is that interest rates are not mean reverting under this model. That is why other models, such as the Hull-White model and the Black-Derman-Toy model are more popular.
On this page, we discuss the Ho-Lee model formula and illustrate how to use it using an example. A Ho-Lee model Excel spreadsheet that can be used to simulate short-term interest rates is available for download at the bottom of the page.
Ho-Lee model formula
Let’s start by presenting the formula
where sigma is the volatility of the interest rate and theta is a time-dependent drift term. Under the Ho-Lee model, the short-term interest rate follows a normal process, where zt is the innovation.
Model calibration
If we want to use the model in practice, the first thing we need to to is collect actual interest rate data. We can then use this data to calibrate the model. That is, we need to estimate theta. To find the value for theta, we determine the value that yields the current term structure. Thus, this model is estimated using the no-arbitrage condition.
Ho-Lee example
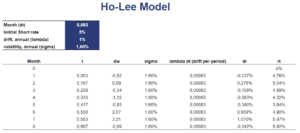
Finally, let’s generate some interest rates using the model. The following table and figure illustrate how we can easily simulate short-term interest rates using the Ho-Lee model. The spreadsheet used to simulate the interest rate path is available for download at the bottom of this page.
Summary
We discussed the HL interest rate model. It is a short-term interest rate model that can be used to generate interest rates that can turn negative. One disadvantage of the approach is that interest rates are not mean-reverting in this model.
Download the Excel spreadsheet
Want to have an implementation in Excel? Download the Excel file: Ho Lee model