Cox-Ingersoll-Ross model

The Cox-Ingersoll-Ross model or CIR model for short, is the most commonly used model to model short-term interest rates. The model was proposed by John Cox, Jonathan Ingersoll, and Stephen Ross in 1985. 

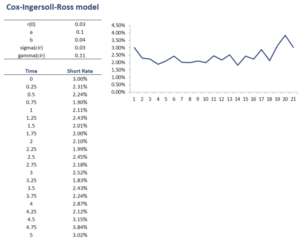
On this page, we discuss the Cox-Ingersoll-Ross model. We also provide an Excel spreadsheet that implements the approach. The Cox-ingersoll-Ross interest rate mode Excel implementation simulates interest rate paths using the formulas below. The spreadsheet can be downloaded at the bottom of the page.

Cox-Ingersoll-Ross model definition

The CIR interest rate model is the simplest and most commonly used model that avoids negative interest rates. Similarly to the Vasicek model, on which the CIR model is based, it models interest rates using a single risk factor. This factor captures market risk and determines the change in the interest rate. 

The model is described using the following equation

    $$dr_t = a(b-r_t)dt + \sigma \sqrt{r_t}dW_t$$

This is a stochastic differential equation where Wt is a Wiener process (capturing the market factor), a is the speed of adjustment, b is the mean to which the interest rate reverts, and sigma is the volatility. 

Similarly to the Vasicek model the term a(b-rt) is the drift factor. Now, the factor \sigma \sqrt{r_t} prevents the interest rates from becoming negative. This will be the case as long as a and b are also positive. It is also possible to impose that interest rates cannot become zero by adding an additional requirement that

    $$2ab >= \sigma^2$$

Often, the resulting interest rate returns are said to follow a CIR process. Another advantage of the CIR model is that it is also possible to derive the distribution of the future values of the CIR process.

Cox-Ingersoll-Ross model Excel

The best way to become familiar with the Cox-Ingersoll-Ross model is to simulate some interest rate returns using the model. To do this, we can make use of a simple Excel spreadsheet. 

Cox-Ingersoll-Ross-Model

The CIR model in Excel can be accessed below. Parameter estimation of a, b, and sigma is similar as in the case of the Vasicek model and can be done using an ordinary least squares (OLS) regression.

Summary

We discussed the CIR model. The model is an extension of the Vasicek model in that it does not allow interest rates to turn negative. Given the recent financial crisis, however, such a restriction may be too restrictive at times, suggesting the Vasicek model is a better alternative.

CIR model calculator

Want to have an implementation in Excel? Download the Excel file: Cox-Ingersoll-Ross