Continuing Residual Income
Continuing Residual Income (CRI) is a modification of traditional residual income. CRI takes into consideration the fact that residual income cannot grow at a constant rate indefinitely. Instead, we can expect that residual income will gradually decrease as competitors enter the market and profit margins are under pressure. Thus, instead of assuming a constant growth rate, we use a so-called persistence factor.
On this page, we discuss how to calculate the present value of residual income based on continuing residual income. We discuss 4 different cases and implement all 4 using a spreadsheet. The Excel file can be downloaded at the bottom of the page.
Continuing residual income definition
Continuing residual income is defined as the income that is expected over the long run. It is not constant, but rather decreasing over time. The speed at which residual income decreases depends on the fortunes of the industry as well as the sustainability of the specific firm’s competitive advantage. The rate at which the residual income is expected to decrease is called the persistence factor, denoted with the greek symbol omega. The persistence factor will vary between 0 and 1.
The persistence factor will be higher if
- the company has a low dividend payout ratio
- high persistence is common in the industry
The persistence factor will be lower if
- the return on equity is higher (attracting more competitors)
- there are significant levels of nonrecurring items
- there are high accounting accruals
Continuing residual income formula
To calculate the value of the company using continuing residual income requires two formulas. First, we note that the value of the company consists of three components:
Second, to calculate the PV of continuing residual income in year T-1, we need the following formula
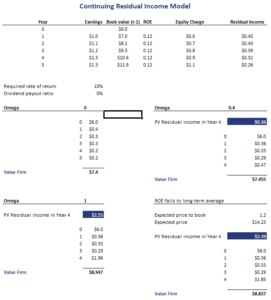
Depending on the value we choose for the persistence factor, we can distinguish 4 cases:
- Residual income persists at the current level forever (omega = 1). In that case, the present value of residual income equals the present value of a perpetuity
- Residual income drops immediately to zero (omega = 0). In that case the present value of residual income in T-1 is residual income in year T discounted at the required rate of return
- Residual income declines over time to zero. This is the case when the omega is a value between zero and one.
- Residual income declines to the long-run level in a mature industry.
In the last case, we don’t rely on the above formula with a persistence factor. Instead we use a formula that we implement below in the Excel example.
Continuing residual income example
The discussion above has been overwhelming. The following example will show that applying the model is very straightforward. The following table implements the approach using an Excel spreadsheet. The file is available for download at the bottom of the page.
Summary
We discussed CRI, a modification of the traditional residual income approach that does not assume growth in residual income is constant in perpetuity.
Residual income calculator
Want to have an implementation in Excel? Download the Excel file: CRI calculator