After-tax Standard Deviation

The after-tax standard deviation and after-tax return should be calculated when taxes apply. Both can easily be calculated once you know the dividend tax and the capital gains tax. After-tax returns and after-tax risk can have a significant impact on the efficient frontier. In particular, allocations to tax inefficient assets such as high yield bonds will usually decrease. They can still play a role, however, if the correlation with other assets in the portfolio is sufficiently low.

After-tax standard deviation

On this page, we discuss how to calculate the after-tax return, how to adjust the current market value to reflect unrealized gains (embedded tax liability) or losses (embedded tax asset), and how to calculate the post-tax standard deviation. We provide an Excel template at the bottom of the page that implements the approach.

Multi-step after-tax return calculation

First, let’s have a look at the calculation of the after-tax return. This approach should be used if the investor is taxable. 

A simple example is the case where the investor does not receive a dividend, but only pays a capital gains tax. Suppose the return is 5% and the capital gains tax is 20%. In that case, the after-tax returns equals

    $$ 3\% = 5\% \cdot (1 - 20\%) $$

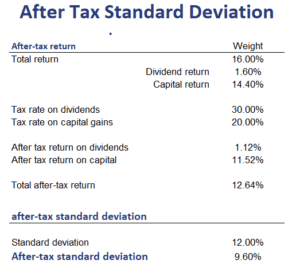
In the case of a dividend, the approach is the following. First, we calculate the dividend income. Suppose we generate a return of 16%, which consists of a capital gain of 14.4% and a dividend of 1.6%.

In that case, the after-tax dividend return will be (assuming a dividend tax rate of 30%)

    $$ 1.12\% = 1.6\% \cdot (1 - 30\%) $$

The after-tax capital gain return will be (assuming a capital gains tax rate of 20%)

    $$ 11.52\% = 14.4\% \cdot (1 - 20\%) $$

The total after-tax return is 12.64%.

After-tax standard deviation calculation

The post-tax standard deviation is easily calculated. We simply take the pre-tax standard deviation. Assuming a capital gains tax of 20% and a standard deviation of 12%, the after-tax standard deviation equals

    $$9.6\% = 12\% (1 - 20\%)$$

Interestingly, taxes cushion the impact of taxes on after-tax standard deviation.

Summary

Taxes complicate the portfolio optimization process. Return and risk need to be considered on both a pre- and an after-tax basis, although correlations will be unaffected by taxes.