Contribution to Portfolio Variance
Absolute risk measures focus on the size and composition of absolute portfolio variance (i.e., without reference to any benchmark variance). This approach is part of a more general framework called risk budgeting. Risk budgeting is a process by which the total risk of a portfolio is allocated to constituents of the portfolio in the most efficient manager. To be able to do this, we have to be able to calculate the contribution to portfolio variance of each constituent.
On this page, we discuss absolute risk attribution and the contribution to variance formulas. A calculator in Excel is available for download at the bottom of the page.
Contribution to portfolio variance formula
The contribution of asset i to portfolio variance (CVi) is given by the following equation:
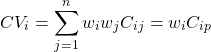
where wj is asset j’s weight in the portfolio, Cij is the covariance of returns between asset i and asset j, and Cip is the covariance of returns between asset i and the portfolio:
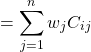
The portfolio variance is the sum of each asset’s contribution.
Contribution to variance example
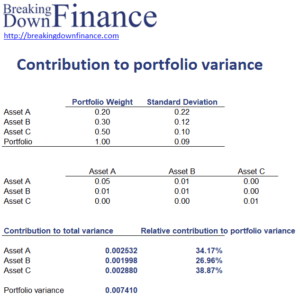
Let’s turn to an example to illustrate the necessary inputs and calculations. To keep things simple, let’s consider a simple portfolio with only three assets. In the table, we provide all the inputs and perform the necessary calculations. We calculate both the absolute contribution as well as the relative contribution to variance.
The spreadsheet is available for download at the bottom of the page
Summary
We discussed how the covariance matrix and the asset’s weights can be used to determine the contribution to variance of individual assets. These results can be used to perform risk budgeting.
Download the Excel spreadsheet
Want to have an implementation in Excel? Download the Excel file: Contribution to variance example