Monte Carlo Forward Rate Simulation

Monte Carlo Forward Rate Simulation is a method for pricing fixed income securities. The approach involves randomly generating a large number of interest rate paths. Typical models used to simulate the interest paths include the Vasicek model and the Cox, Ingersoll, and Roll model. A key feature of these kinds of forward rate simulation approaches is that the cash flows can be path dependent. 

On this page, we discuss the method in broad terms and discuss a simple example that illustrates what the approach looks like in practice. The spreadsheet used to implement the example is available for download at the bottom of the page.

Monte Carlo interest rate simulation

Some fixed income securities’ value is path dependent. One example of path dependent fixed income securities are mortgage-backed securities (MBS). The mortgages that make up the MBS often have the ability to refinance the mortgage. When this happens, the homeowners repay the current mortgage. This results in prepayment risk. This prepayment risk depends not only on the level of interest rates, but also the path interest rates took to get there. 

If interest rates have been low in the past, many homeowners will already have refinanced in the past. In that case, they are unlikely to refinance again, despite the fact that interest may become low a second time.

Monte Carlo rate simulation example

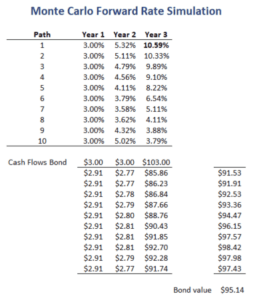
The value of the bond under the Monte Carlo rate simulation is equal to the average of the values of the different paths that are generated. To illustrate how this works, suppose we generate a set of 10 paths. The paths are reported in the following table.

Monte-Carlo-Forward-Rate-Simulation

Then, we use the simulated forward rates to discount the cash flows use each of the paths. The average value of the bond under each of the paths is then the estimated bond price. It is important to understand that each cash flow is discounted at its respective path-specified rate.

Summary

We discussed Monte Carlo rate simulation to price a bond. The main advantage of this approach is that we can use the approach to value bonds whose value is path-dependent.