Market timing

How to time the market? Market timing, together with security selection, are the holy grails in investing. Market timing consists of entering and exiting the market at the right time, avoiding the corrections and riding the bull markets. On this page, we provide the market timing definition, show how to test whether a manager has timing ability, and provide some warnings for investors wanting to time the market.

Market timing definition

A market timer tries to get in and out of the stock market at the right time. This is different from security selection, where the manager tries to select securities that are undervalued, in the hope that the price will increase in the future. A market timer will try to adjust his or her market beta in anticipation of the stock market evolution. In particular, a market timer is successful if he or she can lower his beta before stock markets go down, and increase his beta just before stock markets go up again.

In the case of volatility timing, he manager tries to time the level of volatility in the market. This is because periods of high volatility cause the portfolio to be very volatile. By avoiding these periods, the manager can improve risk-adjusted performance. To see this, let’s consider the Sharpe ratio.

$textrm{Sharpe ratio}= frac{E(r_m - r_f)}{sigma(r_m - r_f)}$

By timing volatility, the manager can lower the denominator of the Sharpe ratio. For a given return, the Sharpe ratio will improve. To forecast future volatility, the manager can use a GARCH model or EWMA.

Market timing example

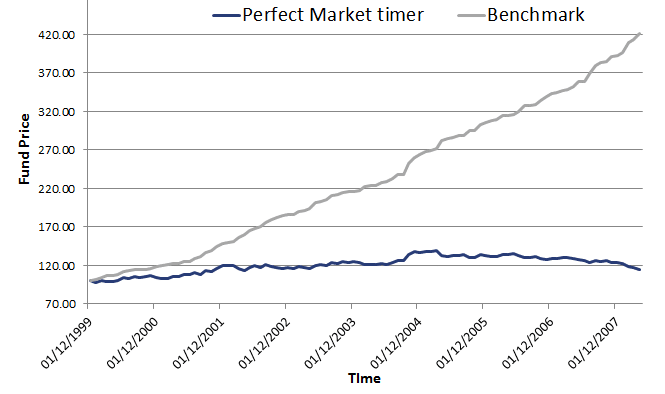
Turning back to market timing. Above we discussed the beta of the portfolio, and argued that the manager should lower his beta when stock markets are about to go down, and increase his beta when he expect markets to go up. Let’s consider an example. Suppose the manager exits the market completely in the case of a bear market. In that case his beta is 0 in the case of a bear market. Conversely, when the market is about to go up, the manager takes leverage so that the beta of his portfolio equals 2.

Next, let’s assume there’s a correction of 10%, i.e. the S&P 500 goes down 10%. In that case the manager’s portfolio will go down

Hence, the manager’s portfolio doesn’t drop in value. Now let’s assume the market goes up 20%, and the manager has a beta of 2.

The manager generates a 40% return! Clearly, the returns to market timing can be big. In this case of perfect market timing, the manager doesn’t lose any money during the bear market and makes a lot of money during the bull market.

Measuring market timing

There are two models that are used to measure market timing. The first model is the so-called Henriksson-Merton model. In this case, the manager is expected to have a different beta during up and down months, which are defined using the market excess return. In particular, up months are defined as months when the excess return is positive. When the market excess return is negative, that months is considered a down month. The model in this case is

$(r_{i,t} - r_{f,t}) = alpha + beta_1 cdot (r_{m,t} - r_{f,t}) + gamma cdot D_t cdot (r_{m,t} - r_{f,t}) + epsilon_t$

Where D_t is the dummy, which is 0 during a negative month, and 1 during a positive month. γ measures the market timing ability. When this value is positive and significant, the manager has market timing ability.

The other model is the Treynor-Mazuy model.

$(r_{i,t} - r_{f,t}) = alpha + beta_1 cdot (r_{m,t} - r_{f,t}) + gamma cdot (r_{m,t} - r_{f,t})^2 + epsilon_t$

The Treynor and Mazuy models measures the amount of convexity in the manager’s returns. It tests whether the manager can successfully increase its exposure when markets go up, and decrease it again when markets go down.

Risks of market timing

There are several risks involved when timing the market. First, there’s the likelihood of missing the rebound, even if you had successfully anticipated the correction. Second, trading leads to increased transaction costs, which should also be earned back when performing market timing. Finally, there’s the difficulty of timing itself. It is very hard to time the market consistently. People may get it right once by chance, but it’s harder to consistently time the market correctly.

Summary

Timing is very difficult and research suggests managers are not able to do it, on average. Volatility timing may be easier to implement for most investors. In addition there are also risk involved when trying to time the market. In particular, one may miss the rebound. Finally, we discussed the Henriksson and Merton model (1981) and the Treynor and Mazuy model (1966), which are widely used to test for timing ability.