Vega Notional of a Variance Swap

The Vega notional of a variance swap is the market convention used to quote the notional on a variance swap. While variance swaps are discussed in more detail elsewhere, we discuss here why vega notional is used by practitioners and how this metric can be inferred from the variance notional of a variance swap. The variance notional of a variance swap represents the profit or loss per point difference between implied variance (K²) and realised variance (sigma²).

At the bottom of the page, we include a simple numerical example in Excel that allows us to convert variance notional into the vega notional.

Vega notional definition

Recall that vega is one of the greeks used in option pricing. Vega refers to the change in an option’s price per a 1% change in volatility. Thus, vega provides a natural way to think about the return for volatility when discussing volatility-based derivatives.

Vega notional is related to variance notional, so we can easily convert variance notional to vega notional and vice versa. In particular, the variance notional equals:

    $$ \textrm{variance notional} = \frac{\textrm{vega notional}}{2\cdot \textrm{strike price}} $$

Thus, the profit or loss (P/L) on a variance swap using the vega notional can be calculated as follows:

    $$ P/L = N_{\textrm{vega}} \cdot( \frac{\sigma^2 - K^2}{2K}) $$

where K is the variance strike, and sigma² is the realised variance when the variance swap expires.

Example

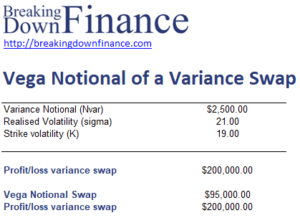
Let’s illustrate the calculation of the variance notional using the vega notional using a simple example. We also illustrate how to use the vega notional to calculate the profit or loss on the variance swap. The Excel file is available for download at the bottom of the page.

Vega Notional of a Variance Swap

Summary

We discussed vega notional, the standard way of quoting the notional of variance swaps. For more details on variance swaps, see the page dedicated to these derivatives.